回顾
之前我们已经学过了逻辑回顾和浅层的神经网络,下面我们简单回顾一下。
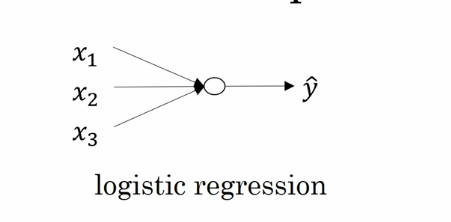
上面是一个逻辑回归的流程,我们输入样本特征,得到一个预测值。 这就是一个最简单的神经网络 (只有一个节点的神经网络)。 那么扩展开来我们看一下神经网络是什么样子的。 先来看我们学到的浅层神经网络,也就是只有一个隐藏层的神经网络。
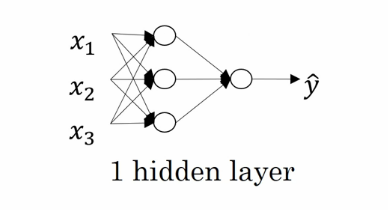
这是一个单隐藏层的的神经网络。 最左边的事输入层 (输入样本特征),最右边的是输出层 (输出预测值),中间的是隐藏层,之所以叫隐藏层是因为它的计算过程我们是看不见的。隐藏层和输出层的每一个单元都是一个逻辑回归。 也就是每一个单元都有一个 y=wx +b 的这么一个公式。其中 x 是特征向量,y 是预测值,w 和 b 是参数。 而机器学习要学的就是 w 和 b 这两个参数,使得计算出的预测值与真实的值相差最小。 根据梯度下降算法,我们会随机初始化每个单元的 w 和 b,然后一步一步减少 w 和 b 的值以找到最优解。 在神经网络中,每一层的计算结果都是下一层的输入。 像神经元一样一步一步的向下传递,一直到最后的输出层。所以科学家们把它叫做神经网络。
什么是深度学习
深度学习是一个很唬人的名字,其实这个名字有碍于人理解它的本质。 深度学习其实就是一个多隐藏层的神经网络。 只是以前不知道那些科学家怎么想的就起了个这高大上的名词。 看下图:

这就是一个有 3 个隐藏层的神经网络,这也是一个深度学习应用。

这是一个卷积神经网络的例子,用来做人脸识别的。 关于卷积神经网络我们以后在谈论,它是深度学习的一个分支。 我们在这里用人话简单说一下它的过程。 我们可以把前几层的神经单元当成是一些探测器。例如上图我们看输入层输入了一张图片,然后第一个隐藏层识别出了一些浅层的边框,把他们输入到第二个隐藏层中继续识别,我们识别出了一些人体器官。然后到下一层,组合成人脸。最后到输出层计算出最终结果。 大家都说深度学习很想是人脑。 因为人脑识别图片的过程就是先识别浅层信息,然后一点点识别更深层的东西。
前向传播
深度学习中有前向传播和后向传播两种操作。 分别对应了计算预测值 y 以及计算每个单元的 w 和 b 对损失函数的导数 (斜率) 以在梯度下降算法中找到合适的步长。其实这也象征了深度学习算法的工作流程,我们先来看前向传播。我们之前说在神经网路中,每一层的输出都是下一层的输入。 所以我们要分别计算每一层的每一个单元的结果。也就是上面说的每一层的每个单元都有 y=wx+b 这么一个函数。 我们计算出结果以后把这些结果作为特征输入给下一层。一直到最后的输出层,计算出预测值 y。 这就是前向传播的过程。这个过程比较容易理解,重要的是反向传播。
反向传播
反向传播是为了求导数 (斜率) 而存在的。回归一下我们在逻辑回归中学到的原理。 算法是要不停的变换 w 和 b 的值来找到预测值与实际值相差最小的那个 w 和 b。 那么每一次我们按什么规则变换 w 和 b 呢? 这就是导数的意义,也就是斜率。 我们看梯度下降算法,根据之前的学习我们知道梯度下降算法就是用来找 w 和 b 的。
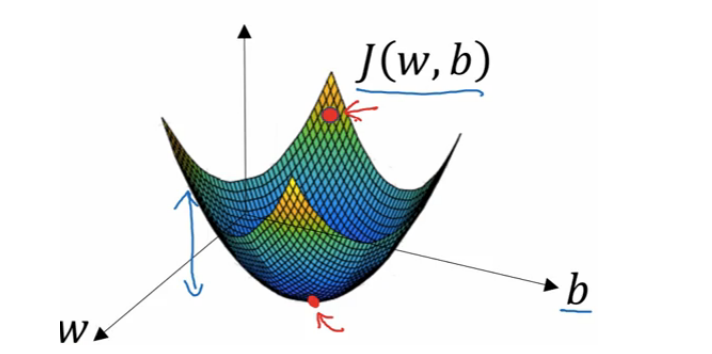
J 是全局成本函数,它衡量预测值与真实的值得差距。 它是一个凸函数,在图中就像一个大碗一样。 也就是说他有最小值,也就是全局最优解。我们要不停的减少 w 和 b 的值来一步一步的向下走,一直走到全局最优解的位置上。 那么计算该怎么减少 w 和 b 的值呢,我们有下面的公式。
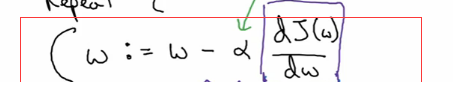
可以看到每一次,w 都会减去学习率乘以 J 对 w 的导数 (斜率)。学习率是我们的超参数,也就是我们运行算法的时候认为的设定的值,一般是 0.01 开始实验。 所以关键就在导数上了。 计算出导数就是反向传播的目的。 在逻辑回归中我们只有一个单元,所以也就是只有一个公式即 y=wx +b. 所以我们只需要计算 J 对 w 和 b 的导数就可以了。 但是在神经网络中, 我们每一个隐藏层都有很多个单元,每个单元都有一个属于自己的 y=wx+b。 那么这些 w 和 b 该怎么办? 就是根据反向传播原理。 我们从输出层开始计算,也就是从右向左计算。 计算出每一个 w 和 b 对全局成本函数 J 的导数出来。
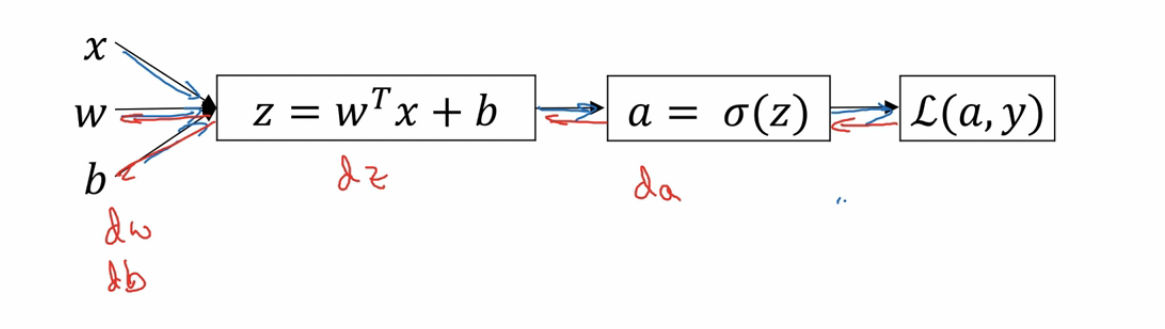
上面是一个最简单的反向传播的例子,也是一个逻辑回归的反向传播。 其中 z 是预测值,a 是预测值经过激活函数变换后的结果,L 是全局成本函数。我们从右边开始计算,先计算出 L 对 a 的导数也就是 da。然后通过 da 计算出 L 对 z 的导数也就是 dz。然后通过 dz 计算出 L 对 w 和 b 的导数 dw 和 db。这就是反向传播过程。 神经网络中通过这种方式分别计算出全局成本函数对每一个神经单元中的 w 和 b 的导数。 这下在一轮梯度下降的迭代中,我们就是可以确定每个单元上该如何变换 w 和 b 的值以完成梯度下降过程了。
参数和超参数
这是一个名称约定,一般我们把 w 和 b 叫做参数。而像学习率这种人为定的值叫做超参数。 同样的还有梯度下降的迭代次数。正则项 L1 和 L2,每一次使用的激活函数,每一层有多少个节点,有多少层,初始化 w 和 b 的方式等等。这些都是我们在运行深度学习的时候需要人工设置的。 而我们的建模过程,就是需要不停的去试试试这些参数以找到最合适的模型。
总结
到这里最基础的东西结束了,之后开始写调参相关的内容,也就是怎么调整我们的超参数。
版权声明:本文由[孙高飞]发表于https://testerhome.com/wiki/deeplearning
如有侵权,请联系commuinty@eolink.com删除。