深度学习基础 --超参数：指数加权平均

李晓超

前言

上一篇我们说通过 mini batch 的方式来为梯度下降算法增速。这次说一说指数加权平均。它同样是用来给梯度下降增速的。在我们的正常的梯度下降中，不论是 mini batch 还是 full batch，梯度下降的效果大概是下面这个样子的。

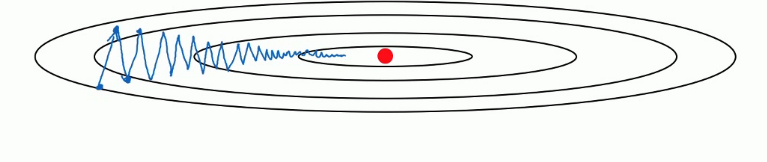
梯度下降算法就像是上面这个图一样，像一个碗一样。这是我们优化成本函数 J 的方式，不停的更新 w 和 b 的值。让函数移动到最下面的那个红色的点，也就是全局最优解。在这个过程中在纵轴上我们是上下波动的，横轴上我们不停的像最优解移动。在这中间我们发现纵轴上下波动的太大导致我们在横轴上的移动速度不是很快。这就需要我们增加迭代次数或者调大学习率来达到最后到达最优解的目的。但是调大学习率会导致每一次迭代的步长过大，也就是摆动过大，误差较大。而增加迭代次数则明显的增加了训练时间。这时候指数加权就出现了。

动量梯度下降法

我们在之前的学习中知道梯度下降是一个优化成本函数 J 的过程，不停的更新 w 和 b 的参数来是成本函数 J 最小。公式是这样的：y = wx + b。每一次迭代都更新 w 和 b 的值，让 w = w - 学习率 *J 对 w 的导数。那么指数加权就是在更新 w 的时候做一些手脚。看下图。

可以看到我们多了一个求 Vdw 和 Vdb，分别在对 w 和 b 的导数上求指数加权平均。然后更新 w 和 b 的时候不再是减去学习率 * 导数了，而是导数的指数加权平均值。其中β就是加权。这也是我们的超参数之一。一般设置为 0.9. 它的效果差不多是下面这样的。

蓝色部分是正常的梯度下降，红色部分是增加了指数加权平均的梯度下降，增加了指数加权后会减少纵轴的上下摆动从而让横轴上更快的移动来达到增速的作用。那么到底什么是指数加权呢？

指数加权平均值

举例说明，下面是一个同学的某一科的考试成绩：
平时测验 80，期中 90，期末 95
学校规定的科目成绩的计算方式是：
平时测验占 20%；
期中成绩占 30%；
期末成绩占 50%；
这里，每个成绩所占的比重叫做权数或权重。那么，
加权平均值 = 80*20% + 90*30% + 95*50% = 90.5
算数平均值 = (80 + 90 + 95)/3 = 88.3

所以这就是指数加权平均值了。在 t 时刻，根据实际的观测值可以求取 V(t)：V(t) = βY(t) + (1-β) EWMA(t-1)，t = 1,2,…..,n；其中，V(t) t 时刻的估计值 (也就是指数加权平均值)；Y(t) t 时刻的测量值；n 所观察的总的时间；β(0 < β <1) 表示对于历史测量值权重系数。之所以称之为指数加权，是因为加权系数β是以指数式递减的，即各指数随着时间而指数式递减。用 n 表示为β = 2/(n+1)。
物理意义：系数β越接近 1 表示对当前抽样值的权重越高，对过去测量值得权重越低，估计值 (器) 的时效性就越强，反之，越弱；另外，V 还有一定的吸收瞬间突发的能力，也即平稳性，显然随着β减小，参考过去测量值的程度更多一些，平稳性增强，反之则降低。

通过这样一个公式，比如我们现在有 100 天的温度值，要求这 100 天的平均温度值。24，25，24，26，34，28，33，33，34，35……….32。
我们直接可以用公式：

化简开得到如下表达式：

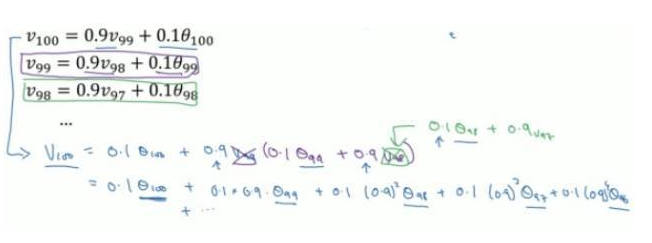
通过上面表达式，我们可以看到，V100 等于每一个时刻天数的温度值再乘以一个权值。
本质就是以指数式递减加权的移动平均。各数值的加权而随时间而指数式递减，越近期的数据加权越重，但较旧的数据也给予一定的加权。
而在我们上面提到的普通平均数求法，它的每一项的权值都是一样的，如果有 n 项，权值都为 1/n。

结尾

之前曾经说过，系数β越接近 1 表示对当前抽样值的权重越高，对过去测量值得权重越低，估计值 (器) 的时效性就越强，反之，越弱。

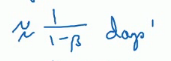
像上图一样，我们 V(指数加权平均值) 是约等于上面的公式的。这里的测量值就是我们的迭代次数。假如我们把β设置为 0.9. 那么根据公式，那么相当于我们对于过去 10 次迭代。1 除以 (1-0.1). 这就是说我们把过去 10 次迭代的 w 和 b 的值算入了指数平均值中。也就是说我们对过去 10 次迭代的数据作为样本，求出了一个平均值作为指数加权。之后根据这个值更新 w 和 b。之所以说有这么一个公式，是因为我们发现指数是随着时间衰减的，太老的数据可以忽略不计了。根据经验，我们设置为 0.9 这个值是比较常见的，也就是用过去 10 次迭代作为参考。

如有侵权，请联系commuinty@eolink.com删除。