研究论文《Sparse Projection Oblique Randomer Forests》
作者:震灵
链接:https://www.zhihu.com/question/501228464/answer/2240195906
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
实至名归的JMLR论文!倘若这篇文章的结论能够未来在机器学习领域得到广泛验证,这篇文章将有很大的可能成为下一代随机森林算法的基准实现方式。
算法原理
基本原理
SPORF的算法原理非常简单,对于一个大小为 ,特征数为
的训练数据矩阵。SPORF算法将随机生成一个包含
的大小为
的矩阵。最终,两个矩阵相乘,就可以得到一个
的训练数据矩阵。将这个矩阵输入到传统决策树算法中,即实现了SPORF算法。
其中,SPORF的随机映射矩阵中的非零元素的数量由一个稀疏度参数 控制。其中,
代表矩阵大小,
代表稀疏度。对于非零元素,SPORF随机选择
进行填充。
与随机森林的关系
SPORF是随机森林的进阶版本,在随机森林的实现中,原始的 个特征会通过随机挑选的方式,保留
个特征,作为决策树构建所使用的特征。因此,随机森林是SPORF的一个特例,即当SPORF的映射矩阵的
列元素,每一列仅有一个元素为1时,SPORF算法会退化为随机森林。
分裂效果实验
下图展示了Trunk这个数据集上SPORF和RF算法的分裂情况。图(A)展示了SPORF收益最高的10个分裂方案,而图(B)展示了RF收益最高的10个分裂方案。从图©和图(D)可以看出,SPORF这种考虑多个变量的分裂方案具有更高的Gini Importance收益,且具有更小的Bayes Error。
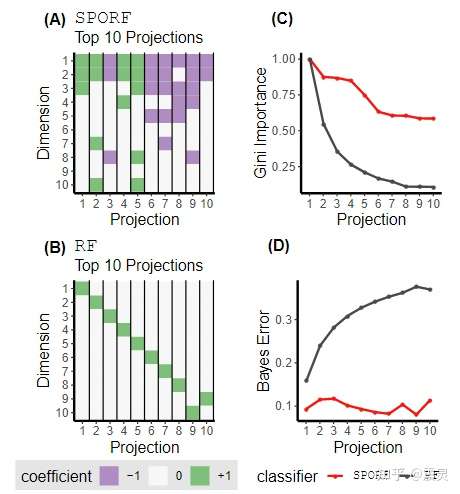
相关实验
SPORF与随机森林对比
为了验证SPORF相比随机森林算法(RF)优势,论文作者选取了"consistency"这个人工数据集进行了初步验证。"consistency"这个数据集的一个特点是随机森林在该数据集上的理论误差下界为 ,即随机森林的误差不会小于下面虚线所示的位置。
而从下面的实验结果可以看出,SPORF可以取得比随机森林理论下界更好的拟合效果。
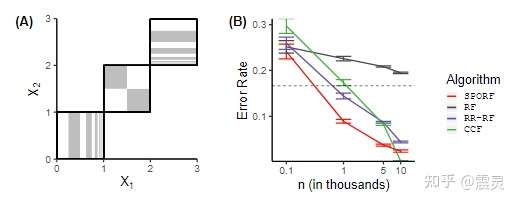
特性验证
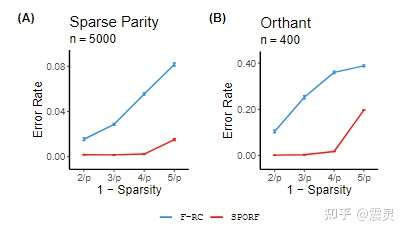
在验证了SPORF相比随机森林的优势之后,作者还在sparse parity和orthant这两个数据集上面进行了探索试验。
首先,作者尝试了sparse parity数据集,该数据集的特点为每个单一维度都无法根据信息增益进行划分,因此正负样本从单一维度上来看是完全无法区分的,这样的数据特性就导致随机森林算法难以在该数据集上有良好的表现。从实验结果来看,尽管随机森林和CCF在该数据集上难以取得令人满意的效果,SPORF在该数据集上效果非常好。
此外,作者还尝试了orthant数据集,相比sparse parity数据集,随机森林可以在该数据集上有良好的表现,但是一些基于倾斜决策树的集成学习算法,例如CCF和F-RC在该数据集上表现较差。相比之下,SPORF的拟合误差则可以和RF保持在同一水平。从而,作者利用上述两个实验证明了SPORF可以适应多种多样的训练场景,具有非常强的拟合能力。
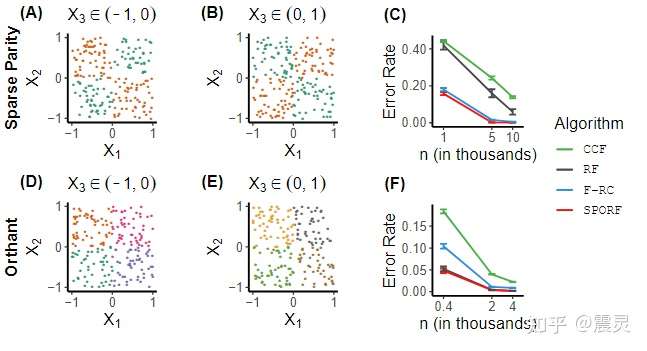
SPORF与F-RC对比
F-RC算法是当前最类似于SPORF算法的随机森林算法,该算法的核心思想也是将一个 的训练数据矩阵映射为一个
的训练数据矩阵。SPORF和F-RC最大的区别在于SPORF算法的稀疏度是控制整个映射矩阵的稀疏度,而F-RC的稀疏度则是控制每一列的稀疏度。也就是说,F-RC要求每一列新特征需要基于相同数量的原始特征进行构建。
下图展示了F-RC和SPORF算法的区别,从图中可以看出,在不同稀疏度的情况下,SPORF远优于F-RC算法。
预测性能
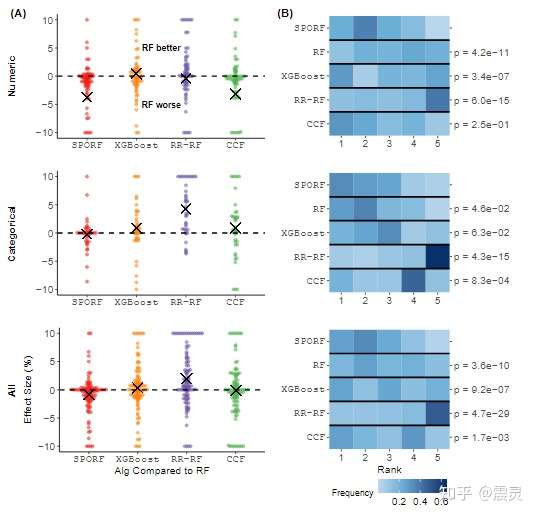
下图展示了五种分类器的预测性能,论文作者使用Cohen’s kappa分数作为分类效果衡量指标,在图(A)中展示了不同分类器与随机森林的相对效果,在图(B)中展示了不同分类器的相对排名统计结果。从两个图中可以看出,无论是在连续型数据集上还是离散型数据集上,SPORF算法都具有良好的表现。
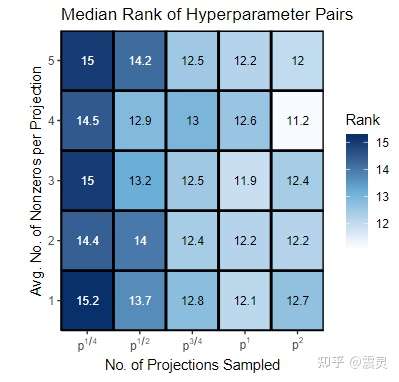
参数分析
下图展示了SPORF引入的两个超参数, 和
在不同数值情况下的预测性能排名。从实验结果来看,当新特征数量
为原始特征数量的平方,即
时,效果最好。但是,鉴于这种情况下会消耗过多的资源,因此SPORF推荐的默认参数为
。至于稀疏度,SPORF推荐的默认参数为
,即每一列新映射特征平均由三个原始特征组成。
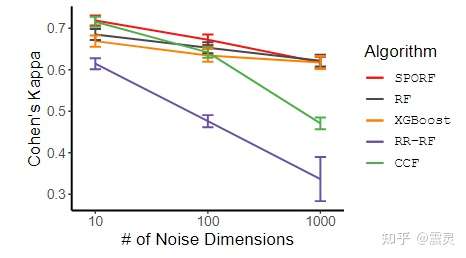
噪声添加
下图展示了添加10-1000维噪声作为训练数据之后,不同学习算法的Cohen’s kappa分数。可以看到在添加了噪声维度之后,SPORF依然保持着最佳的预测性能。
训练时间
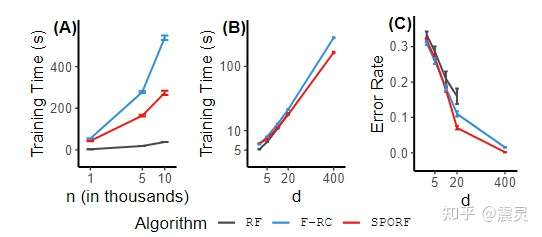
下图展示了SPORF算法不同参数在20维sparse parity数据集上的训练时间,从图中可以看出,随着训练数据量的增加,SPORF算法会比RF算法相对较慢。但是值得注意的是,图(A)的SPORF训练时间是在最优SPORF参数情况下统计得到的。而从图(B)中可以看出,随着映射维度的增加,SPORF的训练时间也会增加。但是值得注意的是,在相同映射维度情况下,SPORF的训练时间和随机森林的训练时间相差无几,而从图©中可以看出此时SPORF的误差明显小于随机森林。通过上述试验,作者向我们证明了SPORF实际上是一种比随机森林更高效的算法。
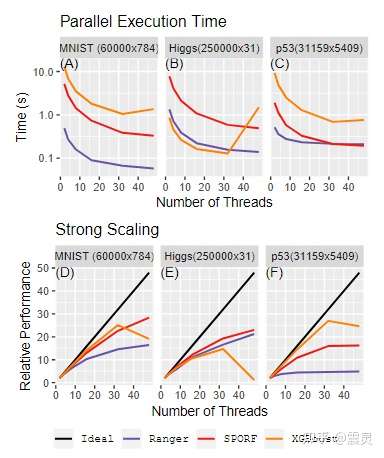
下图展示了SPORF算法的训练时间,从训练时间来看,SPORF算法具有良好的训练时间和并行加速效果。
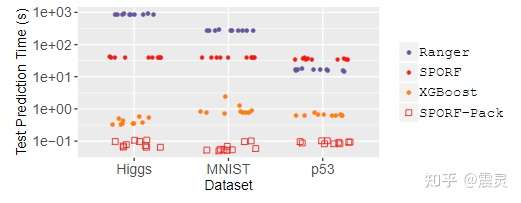
预测时间
下图展示了SPORF算法的预测时间,从预测时间来看,在使用Pack决策树压缩算法增强之后的SPORF-PACK算法具有最短的预测时间。