什么是Floyd-Warshall算法
如果有一个带权图,怎么才能求出图中所有顶点两两之间的最短距离?
使用之前介绍的Dijkstra算法,针对图中每一个顶点都使用一次,也可以做到求出所有顶点之间的最短距离。
但由于Dijkstra算法的代码逻辑较为复杂,所以可以使用Floyd-Warshall(弗洛伊德算法)算法做同样的事情,代码逻辑更简洁,而且两个算法求多源最短路径的总时间复杂度也相同,均为O(n3)。
弗洛伊德算法的英文名称是Floyd-Warshall(不是心理学大师弗洛伊德),专门用于寻找带权图中多源点之间的最短路径。算法的思路是根据图实例中所有顶点,不断引入新的顶点作为中继顶点,借由一个个中继顶点,一步步推导求出所有顶点之间的最短距离。
Floyd-Warshall算法详细步骤
以下算法详细步骤图,均来自公众号"程序员小灰"的文章——《漫画:图的 “多源” 最短路径》
假设有这样一个带权图的邻接矩阵。
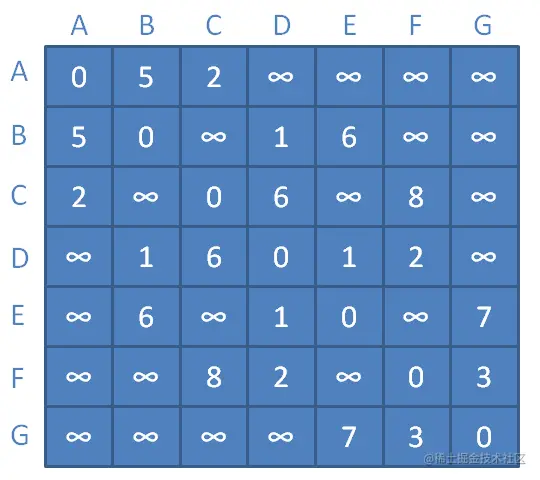
假设按图实例的顶点顺序,以A开始作为邻接矩阵的中继顶点:
顶点B与顶点C之间距离为无限大,此时缩短为顶点A到顶点B距离+顶点B到顶点C的距离=5+2=7。
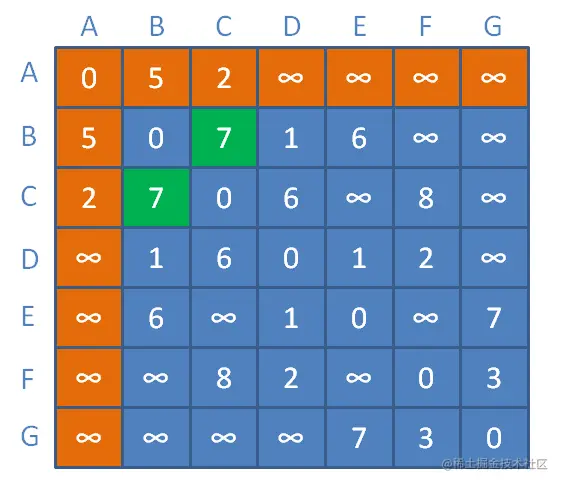
再假设,现在接着引入新的中继顶点,以A、B作为邻接矩阵的中继顶点:
顶点A与顶点D之间距离为无限大,以顶点B作为中继顶点,此时缩短为顶点A到顶点B距离+顶点B到顶点D的距离=5+1=6。
顶点A与顶点E之间距离为无限大,以顶点B作为中继顶点,此时缩短为顶点A到顶点B距离+顶点B到顶点E的距离=5+6=11。
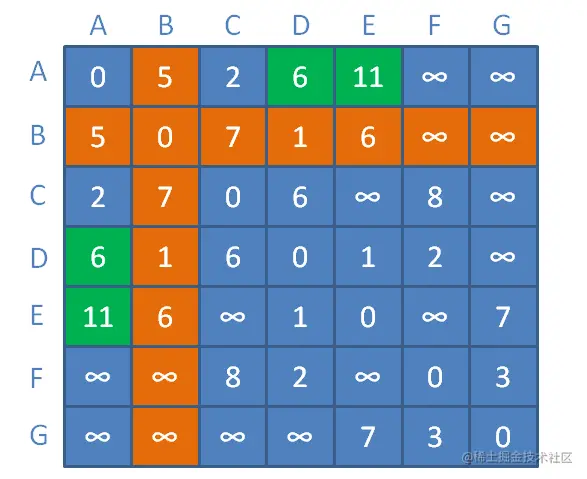
再假设,接着引入新的中继顶点,以A、B、C作为邻接矩阵的中继顶点:
顶点A与顶点F之间距离为无限大,以顶点C作为中继顶点,此时缩短为顶点A到顶点C距离+顶点C到顶点F的距离=2+8=10。
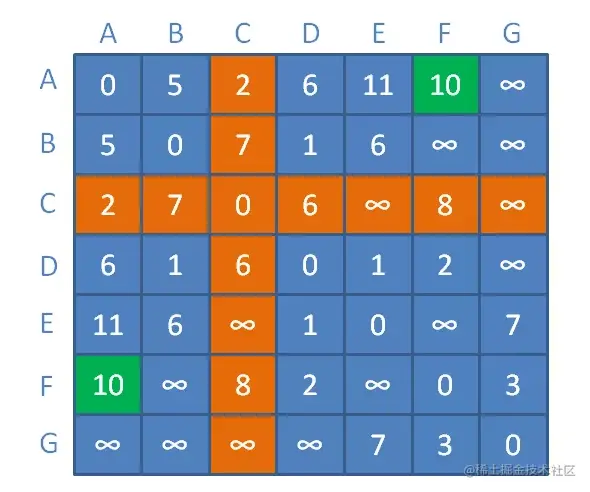
(注:为了简化理解,以上图解过程演示情况仅考虑了顶点A到某个顶点之间的距离,未演示其他任意顶点到某个顶点之间的距离)
重复上面的步骤,不断引入新的中继顶点,刷新邻接矩阵中的临时距离
最终得到如下图实例的距离表:
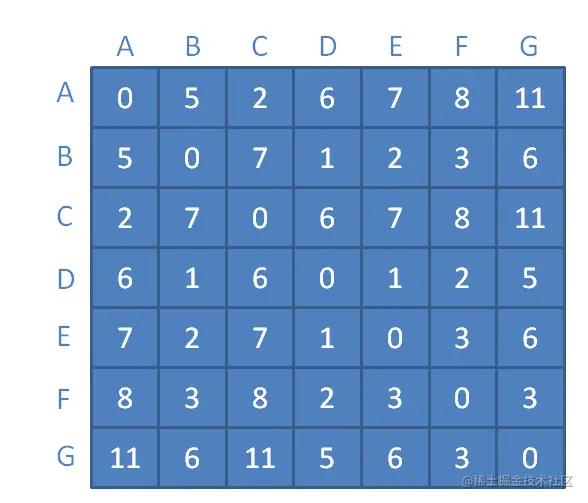
此时,距离表中记录着图中某一个顶点,到任意另外一个顶点的最短距离。
代码实现
/**
* 最短路径算法-弗洛伊德算法
* @param {*} graph 需要计算最短路径的图实例
* @returns {*} 图实例(带权图)的最短路径
*/
export const floydWarshall = graph => {
const dist = []; //创建距离表,存储从起点到每一个顶点的距离(权值)
const { length } = graph; //图实例的顶点数量
// 初始化距离表为图实例每个顶点及其邻接矩阵的距离(权值)
for (let i = 0; i < length; i++) { // 遍历图实例的所有顶点
dist[i] = []; // 将图实例对应的顶点初始化为空矩阵
for (let j = 0; j < length; j++) { // 循环遍历图当前顶点和其他顶点的关系(当前顶点和其他顶点是否有边)
if (i === j) {
// 如果是顶点到自身的距离,这距离是0
dist[i][j] = 0;
} else if (!isFinite(graph[i][j])) {
// 如果这两个顶点之间没有边,就将其表示为 Infinity(无穷大)
dist[i][j] = Infinity;
} else {
// 如果这两个顶点之间有边,则在距离表记录他们的距离(权值)
dist[i][j] = graph[i][j];
}
}
}
//循环更新矩阵的值
for (let k = 0; k < length; k++) { // 将顶点 0 到 k(图实例的长度) 作为中继顶点
for (let i = 0; i < length; i++) { // 循环遍历图实例的所有顶点
for (let j = 0; j < length; j++) { // 循环遍历图当前顶点和其他顶点的关系(当前顶点和其他顶点是否有边)
// i 到 j 的最短路径经过 k
if (dist[i][k] + dist[k][j] < dist[i][j]) { // 计算通过顶点 k 的 i 和 j 之间的最短路径
// const numberToChat = ['A', 'B', 'C', 'D', 'E', 'F', 'G'];
// console.log('k——',numberToChat[k],'i——',numberToChat[i], 'j——', numberToChat[j]);
// console.log('dist[i][j]——',dist[i][j], 'dist[i][k]——',dist[i][k], 'dist[k][j]——', dist[k][j]);
// console.log(`${numberToChat[i]}${numberToChat[j]}=${numberToChat[i]}${numberToChat[k]}+${numberToChat[k]}${numberToChat[j]}`);
dist[i][j] = dist[i][k] + dist[k][j]; // 如果一个最短路径的新的值被找到,我们要使用并存储它
}
}
}
}
return dist; // 处理完所有顶点后,返回图中所有顶点到其他顶点最短路径的结果。
};
代码实例
假如有这样一个图实例:
const graphdemo = [
[0, 5, 2, Infinity, Infinity, Infinity, Infinity],
[5, 0, Infinity, 1, 6, Infinity, Infinity],
[2, Infinity, 0, 6, Infinity, 8, Infinity],
[Infinity, 1, 6, 0, 1, 2, Infinity],
[Infinity, 6, Infinity, 1, 0, Infinity, 7],
[Infinity, Infinity, 8, 2, Infinity, 0, 3],
[Infinity,Infinity,Infinity,Infinity,7,3,0]
]
加入将数组下标转换成对应顶点的辅助常量numberToChar
const numberToChar = ['A', 'B', 'C', 'D', 'E', 'F', 'G'];
取消上述代码实现中的注释部分,并将图实例(graphdemo)传入弗洛伊德算法(floydWarshall)可以得到如下过程结果:
floydWarshall(graphdemo);
/**
VM564:28 k—— A i—— B j—— C
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 5 dist[k][j]—— 2
VM564:30 BC=BA+AC
VM564:28 k—— A i—— C j—— B
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 2 dist[k][j]—— 5
VM564:30 CB=CA+AB
VM564:28 k—— B i—— A j—— D
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 5 dist[k][j]—— 1
VM564:30 AD=AB+BD
VM564:28 k—— B i—— A j—— E
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 5 dist[k][j]—— 6
VM564:30 AE=AB+BE
VM564:28 k—— B i—— C j—— E
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 7 dist[k][j]—— 6
VM564:30 CE=CB+BE
VM564:28 k—— B i—— D j—— A
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 1 dist[k][j]—— 5
VM564:30 DA=DB+BA
VM564:28 k—— B i—— E j—— A
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 6 dist[k][j]—— 5
VM564:30 EA=EB+BA
VM564:28 k—— B i—— E j—— C
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 6 dist[k][j]—— 7
VM564:30 EC=EB+BC
VM564:28 k—— C i—— A j—— F
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 2 dist[k][j]—— 8
VM564:30 AF=AC+CF
VM564:28 k—— C i—— B j—— F
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 7 dist[k][j]—— 8
VM564:30 BF=BC+CF
VM564:28 k—— C i—— E j—— F
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 13 dist[k][j]—— 8
VM564:30 EF=EC+CF
VM564:28 k—— C i—— F j—— A
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 8 dist[k][j]—— 2
VM564:30 FA=FC+CA
VM564:28 k—— C i—— F j—— B
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 8 dist[k][j]—— 7
VM564:30 FB=FC+CB
VM564:28 k—— C i—— F j—— E
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 8 dist[k][j]—— 13
VM564:30 FE=FC+CE
VM564:28 k—— D i—— A j—— E
VM564:29 dist[i][j]—— 11 dist[i][k]—— 6 dist[k][j]—— 1
VM564:30 AE=AD+DE
VM564:28 k—— D i—— A j—— F
VM564:29 dist[i][j]—— 10 dist[i][k]—— 6 dist[k][j]—— 2
VM564:30 AF=AD+DF
VM564:28 k—— D i—— B j—— E
VM564:29 dist[i][j]—— 6 dist[i][k]—— 1 dist[k][j]—— 1
VM564:30 BE=BD+DE
VM564:28 k—— D i—— B j—— F
VM564:29 dist[i][j]—— 15 dist[i][k]—— 1 dist[k][j]—— 2
VM564:30 BF=BD+DF
VM564:28 k—— D i—— C j—— E
VM564:29 dist[i][j]—— 13 dist[i][k]—— 6 dist[k][j]—— 1
VM564:30 CE=CD+DE
VM564:28 k—— D i—— E j—— A
VM564:29 dist[i][j]—— 11 dist[i][k]—— 1 dist[k][j]—— 6
VM564:30 EA=ED+DA
VM564:28 k—— D i—— E j—— B
VM564:29 dist[i][j]—— 6 dist[i][k]—— 1 dist[k][j]—— 1
VM564:30 EB=ED+DB
VM564:28 k—— D i—— E j—— C
VM564:29 dist[i][j]—— 13 dist[i][k]—— 1 dist[k][j]—— 6
VM564:30 EC=ED+DC
VM564:28 k—— D i—— E j—— F
VM564:29 dist[i][j]—— 21 dist[i][k]—— 1 dist[k][j]—— 2
VM564:30 EF=ED+DF
VM564:28 k—— D i—— F j—— A
VM564:29 dist[i][j]—— 10 dist[i][k]—— 2 dist[k][j]—— 6
VM564:30 FA=FD+DA
VM564:28 k—— D i—— F j—— B
VM564:29 dist[i][j]—— 15 dist[i][k]—— 2 dist[k][j]—— 1
VM564:30 FB=FD+DB
VM564:28 k—— D i—— F j—— E
VM564:29 dist[i][j]—— 21 dist[i][k]—— 2 dist[k][j]—— 1
VM564:30 FE=FD+DE
VM564:28 k—— E i—— A j—— G
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 7 dist[k][j]—— 7
VM564:30 AG=AE+EG
VM564:28 k—— E i—— B j—— G
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 2 dist[k][j]—— 7
VM564:30 BG=BE+EG
VM564:28 k—— E i—— C j—— G
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 7 dist[k][j]—— 7
VM564:30 CG=CE+EG
VM564:28 k—— E i—— D j—— G
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 1 dist[k][j]—— 7
VM564:30 DG=DE+EG
VM564:28 k—— E i—— G j—— A
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 7 dist[k][j]—— 7
VM564:30 GA=GE+EA
VM564:28 k—— E i—— G j—— B
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 7 dist[k][j]—— 2
VM564:30 GB=GE+EB
VM564:28 k—— E i—— G j—— C
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 7 dist[k][j]—— 7
VM564:30 GC=GE+EC
VM564:28 k—— E i—— G j—— D
VM564:29 dist[i][j]—— Infinity dist[i][k]—— 7 dist[k][j]—— 1
VM564:30 GD=GE+ED
VM564:28 k—— F i—— A j—— G
VM564:29 dist[i][j]—— 14 dist[i][k]—— 8 dist[k][j]—— 3
VM564:30 AG=AF+FG
VM564:28 k—— F i—— B j—— G
VM564:29 dist[i][j]—— 9 dist[i][k]—— 3 dist[k][j]—— 3
VM564:30 BG=BF+FG
VM564:28 k—— F i—— C j—— G
VM564:29 dist[i][j]—— 14 dist[i][k]—— 8 dist[k][j]—— 3
VM564:30 CG=CF+FG
VM564:28 k—— F i—— D j—— G
VM564:29 dist[i][j]—— 8 dist[i][k]—— 2 dist[k][j]—— 3
VM564:30 DG=DF+FG
VM564:28 k—— F i—— E j—— G
VM564:29 dist[i][j]—— 7 dist[i][k]—— 3 dist[k][j]—— 3
VM564:30 EG=EF+FG
VM564:28 k—— F i—— G j—— A
VM564:29 dist[i][j]—— 14 dist[i][k]—— 3 dist[k][j]—— 8
VM564:30 GA=GF+FA
VM564:28 k—— F i—— G j—— B
VM564:29 dist[i][j]—— 9 dist[i][k]—— 3 dist[k][j]—— 3
VM564:30 GB=GF+FB
VM564:28 k—— F i—— G j—— C
VM564:29 dist[i][j]—— 14 dist[i][k]—— 3 dist[k][j]—— 8
VM564:30 GC=GF+FC
VM564:28 k—— F i—— G j—— D
VM564:29 dist[i][j]—— 8 dist[i][k]—— 3 dist[k][j]—— 2
VM564:30 GD=GF+FD
VM564:28 k—— F i—— G j—— E
VM564:29 dist[i][j]—— 7 dist[i][k]—— 3 dist[k][j]—— 3
VM564:30 GE=GF+FE
**/
/**
return后,dist的结果:
[
[0,5,2,6,7,8,11],
[5,0,7,1,2,3,6],
[2,7,0,6,7,8,11],
[6,1,6,0,1,2,5],
[7,2,7,1,0,3,6],
[8,3,8,2,3,0,3],
[11,6,11,5,6,3,0]
]
**/