过拟合问题是机器学习中经常需要考虑的问题，有两个办法可以解决过拟合问题，一个是增加更多的数据，另一个是使用正则化来简化模型，使得模型在新的数据上有更好的泛化性能。
常用的正则化方法是L1正则化和L2正则化。在介绍L1和L2正则化之前先了解一下什么是范数。
1、范数 norm
范数可以将一个向量转换为一个标量，可以理解为衡量一个向量的长度。在遇到机器学习中的低秩，稀疏模型时，会用到各种范数。范数的公式如下：
p=1时，就是向量的1范数（L1范数），即向量的各个元素的绝对值之和，又称为曼哈顿距离。使用L1范数可以度量两个向量间的差异（绝对误差和）。
p=2时，就是向量的2范数（L2范数），即向量的每个元素的平方之和的平方根，也可以表示向量的长度（模）或两点之间的距离，又称为欧氏距离。L2也可以度量两个向量间的差异（平方误差和）。
关于范数更详细的解释可以移步：
0 范数、1 范数、2 范数有什么区别？963 关注 · 13 回答问题
2、L1和L2正则化
L1范数和L2范数，用在机器学习中就是L1正则化、L2正则化。正则化就是在原损失函数（目标函数）中引入正则项（惩罚项），下面是多样本的添加了正则项的损失公式，其中 λ 是正则化参数，决定了正则项作用的强弱：
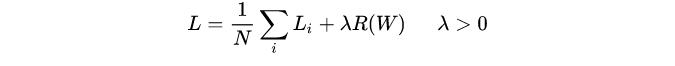
第一项为data loss，第二项为regularization loss。
数据损失部分表示由权重参数构成的模型对训练数据的拟合程度，但是我们更关心的是该模型对测试数据的拟合程度，添加一个正则项可以简化模型并提高模型在测试数据上的泛化性能，即在模型中添加正则项是为了简化模型，而不是拟合数据。
下面分别是添加L1正则项和L2正则项的损失函数：
L1正则化是指权重矩阵中各个元素的绝对值之和，为了优化正则项，会减少参数的绝对值总和，所以L1正则化倾向于选择稀疏(sparse)权重矩阵（稀疏矩阵指的是很多元素都为0，只有少数元素为非零值的矩阵）。L1正则化主要用于挑选出重要的特征，并舍弃不重要的特征。
L2正则化是指权重矩阵中各个元素的平方和，为了优化正则项，会减少参数平方的总和，所以L2正则化倾向于选择值很小的权重参数（即权重衰减），主要用于防止模型过拟合。是最常用的正则化方法。一定程度上，L1也可以防止过拟合。
3、过拟合
我们要用正则化解决的是过拟合问题，那什么是过拟合呢？
当模型为了过度拟合训练集而变得很复杂时，就容易出现过拟合现象。这时模型对训练数据拟合得非常好，但是丧失一般性，趋向于记住而不是学习数据的特征，从而导致模型在新的数据上的表现很差，即泛化能力很差。
当过拟合现象发生，模型会将训练集中的随机出现的噪声也当作有效数据（如下面中的右图，高方差），并对其进行学习和拟合，这就是为什么模型在新数据上的表现会出现退化。
加入了正则项之后，随着正则化强度的增加，过拟合的模型的决策边界会逐渐变得更加平滑（即下面的从右图往左图变化）。下图表示了过拟合和欠拟合的情况：
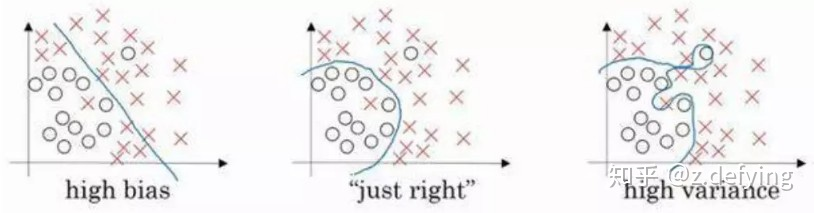
（图来自吴恩达的深度学习课程）
4、防止过拟合
为什么引入正则化项就能防止过拟合呢？其实主要原理就是通过引入权重参数来限制模型的复杂度，从而提高模型的泛化能力。
L2正则项中的 λ 参数越大，模型中的权重矩阵的值就越小。模型中就会有很多隐藏单元的权重值非常小，这些隐藏单元在模型中的影响就变得很小，这就相当于把神经网络简化为一个较小的网络，但是网络深度不变，于是模型就会从过拟合状态向欠拟合状态转换。调整 λ 参数，可以使模型介于过拟合和欠拟合之间。
同时L2正则化可以对大数值权重进行惩罚，这使得没有哪个特征能够单独对整个模型有过大的影响，即每个维度对最终结果的影响都不是很大，使模型把大多数维度上的特征都利用起来，而不是只依赖其中少数几个特征。
在有sigmoid或tanh激活函数的神经网络中，如果学习后的权重参数比较大，那传入激活函数的值就很大，会导致梯度变得非常小，优化模型变得很困难，这时在原来的误差函数上增加一个L2正则项，如果权重过大，就会给损失函数一个较大的惩罚。
总结
偏数学一点的理解就是，正则化对模型的训练增加约束条件，隐式地减小解的空间（权重参数），减小求出错误解的可能性，同时使其不会变得很难优化。
在训练模型时，应该逐渐增大网络的规模，直到在训练集上过拟合，然后使用正则化技巧来解决过拟合问题，然后再继续增大网络规模，继续使用正则化来解决过拟合问题。通过这种方法可以提高模型的准确率。
L1正则化会趋向于选择稀疏矩阵，即只使用一部分特征，而其他的特征都为0；而L2正则化基本上会使用更多的特征，不过每个特征发挥的作用都比较小。在只有少部分特征起重要作用的情况下，可以选择L1范数，因为它会自动地选择重要的特征。如果大部分特征都对结果起作用，即便起的作用很小很平均，这时使用L2范数更合适。
