利用时间序列数据数据做预测,需要抽取特征,其中一类想到频域特征。
基本做法是时间序列数据上做滑动窗口,在每个滑动窗口中做频域变换(如DWT或者FFT),再从变换后的结果中计算(抽取)特征。
比较常见的有哪些特征可以抽取?
作者:水莲
链接:https://www.zhihu.com/question/24021704/answer/2245867156
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
第一种分类
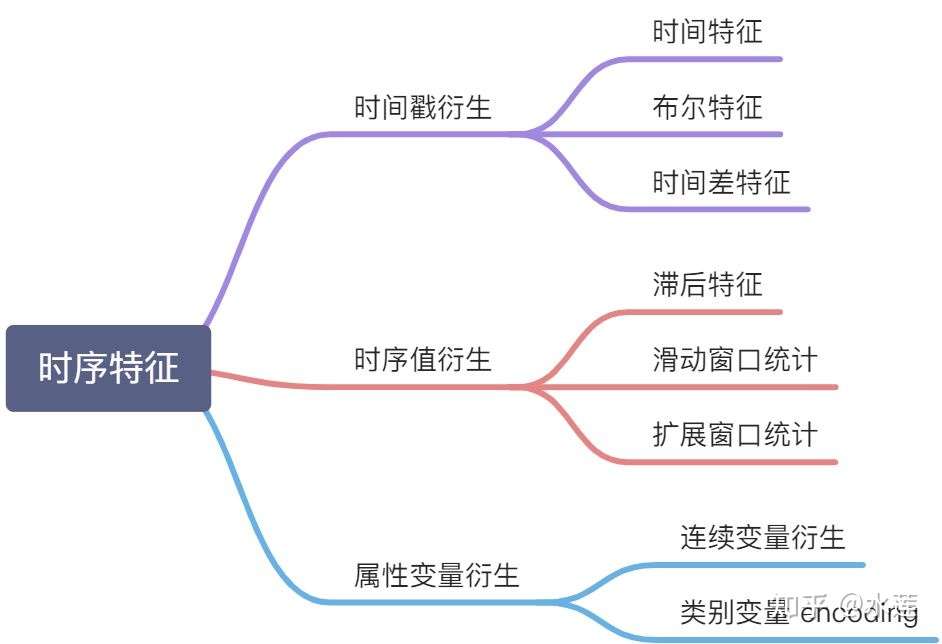
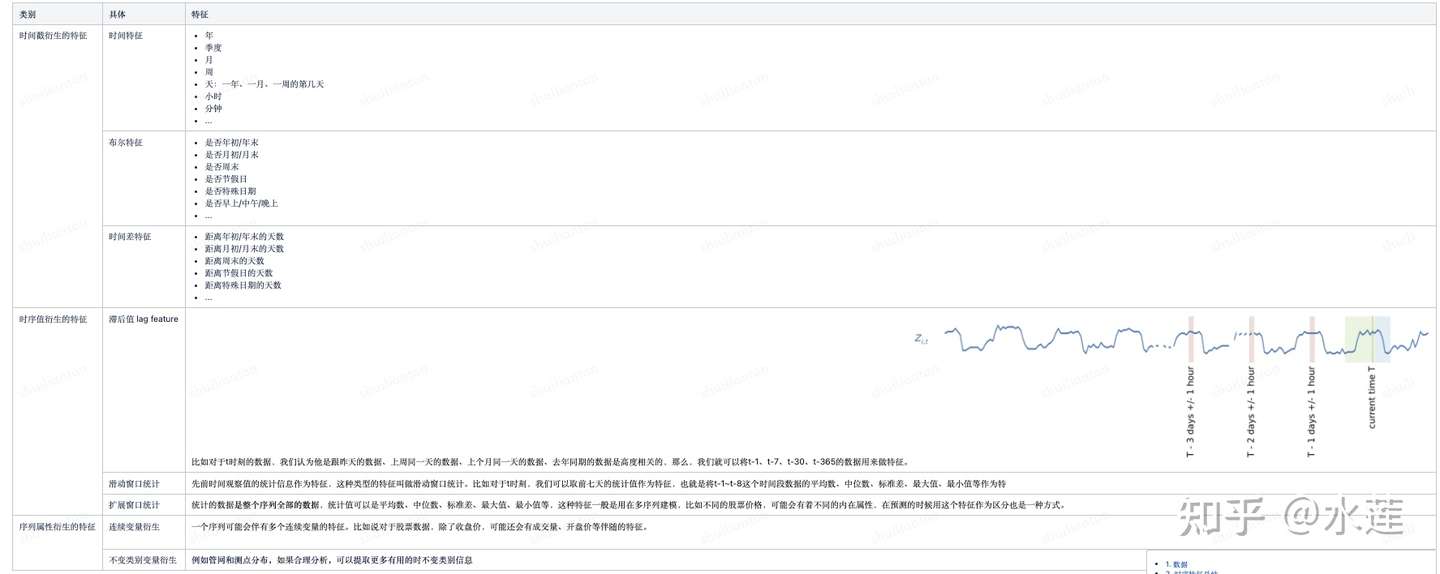
第二种分类
统计域(Statistical Domain)、谱域(Spectral Domain)和时域(Temporal Domain)的角度出发,共容纳数十种特征提取方法:
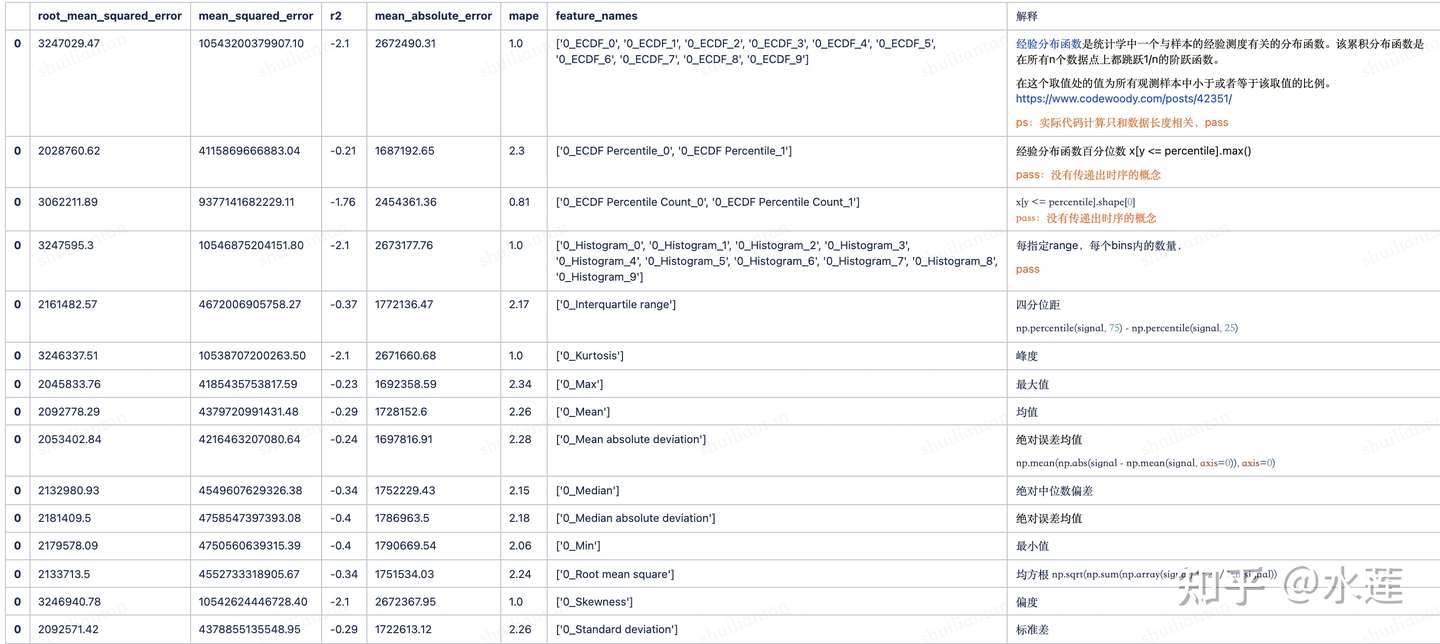
基于统计域的时序特征包含:最大值(Maximum)、最小值(Minimum)、均值(Mean)、中位数(Median)、偏度(Skewness)、峰度(Kurtosis)、直方图(Histogram)、四分位距(Interquartile Range)、绝对误差均值(Mean Absolute Deviation)、绝对误差中位数(Median Absolute Deviation)、均方根(Root Mean Square)、标准差(Standard Deviation)、方差(Variance)、经验分布函数百分位数(Empirical Distribution Function Percentile Count)、经验分布函数斜率(ECDF Slope)等;
基于谱域的时序特征包含:快速傅里叶变换(Fast Fourier Transform)、傅里叶变换平均系数(FFT Mean Coefficient)、小波变换(Wavelet Transform)、小波绝对均值(Wavelet Absolute Mean)、小波标准差(Wavelet Standard Deviation)、小波方差(Wavelet Variance)、谱距离(Spectral Distance)、频谱基频(Spectral Fundamental Frequency)、频谱最大频率(Spectral Maximum Frequency)、频谱中频(Spectral Median Frequency)、频谱最大峰值(Spectral Maximum Peaks)等;
基于时域的时序特征包含:自相关(Autocorrelation)、质心(Centroid)、差分均值(Mean Differences)、差分绝对值均值(Mean Absolute Differences)、差分中位数(Median Differences)、差分绝对值中位数(Median Absolute Differences)、差分绝对值之和(Sum of Absolute Differences)、熵(Entropy)、波峰与波谷距离(Peak to Peak Distance)、曲线覆盖面积(Area Under the Curve)、最大峰值个数(The Number of Maximum Peaks)、最小峰值个数(The Number of Minimum Peaks)、跨零率(Zero Crossing Rate)等。
时序特征库 TSFEL
https://github.com/ElsevierSoftwareX/SOFTX_2020_1github.com/ElsevierSoftwareX/SOFTX_2020_1
直观、快速部署和可重现性: 用于特征选择和定制的交互式用户界面
计算复杂度评估: 在提取特征之前估计计算量
综合文献: 每种特征提取方法都有详细的说明
单元测试: 我们为每个特性提供单元测试
容易扩展: 添加新功能很容易,我们鼓励您贡献您的自定义功能
从统计、时间、谱域上提供超过60种特征
统计类特征
- 经验分布函数ECDF
经验分布函数zh.wikipedia.org/wiki/%E7%BB%8F%E9%AA%8C%E5%88%86%E5%B8%83%E5%87%BD%E6%95%B0
是统计学中一个与样本的经验测度有关的分布函数。该累积分布函数是在所有n个数据点上都跳跃1/n的阶跃函数。在这个取值处的值为所有观测样本中小于或者等于该取值的比例。
Python: 获取经验分布(ECDF)的方法www.codewoody.com/posts/42351/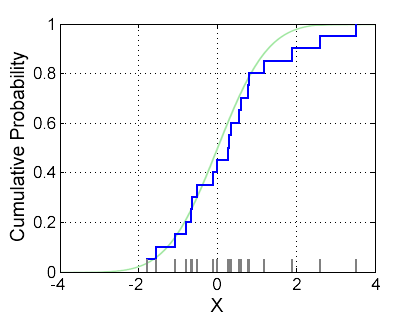
2. 经验分布函数百分位数
$$
x, y = calc_ecdf(signal) x[y <= percentile].max()
$$
谱域类特征
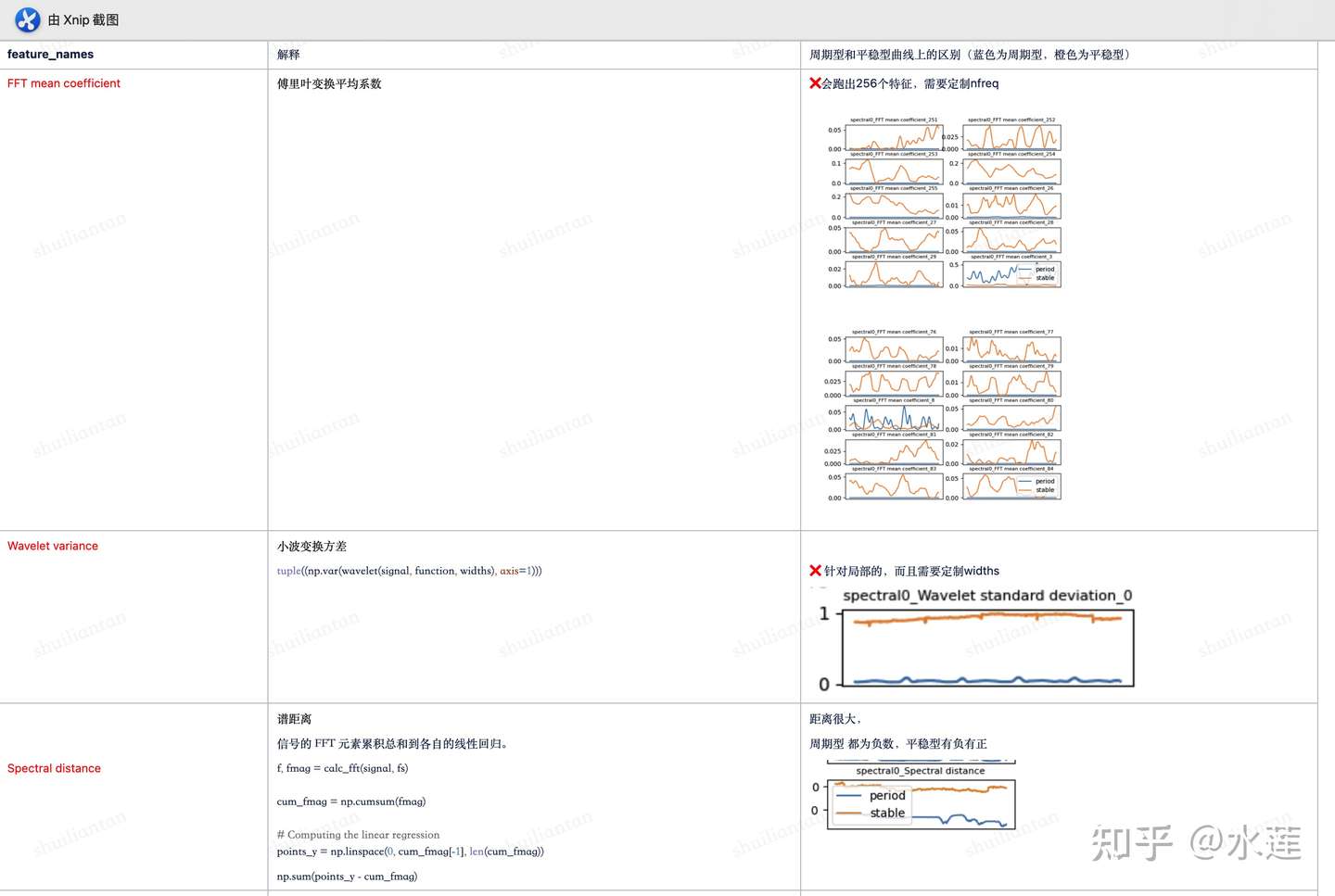
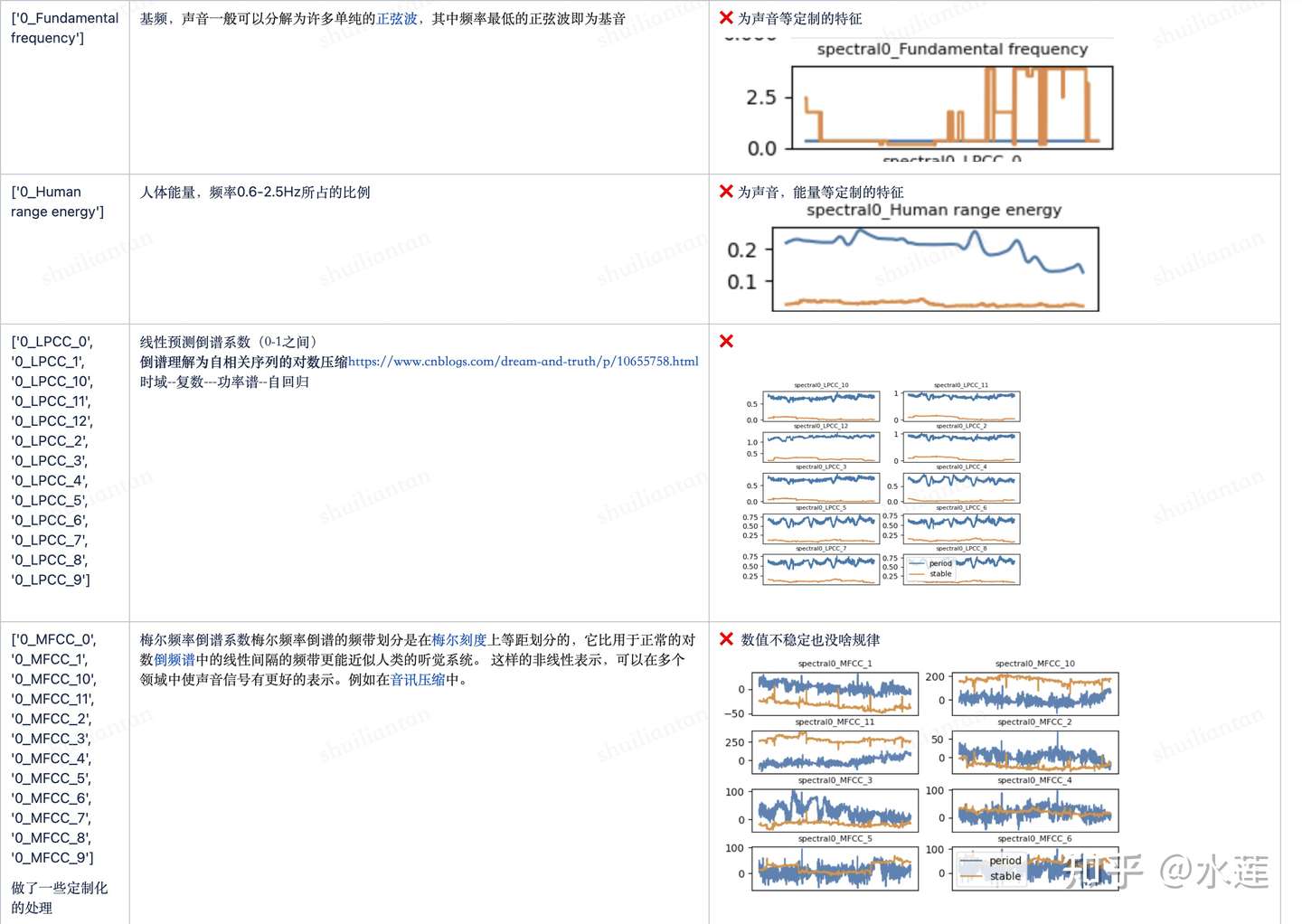
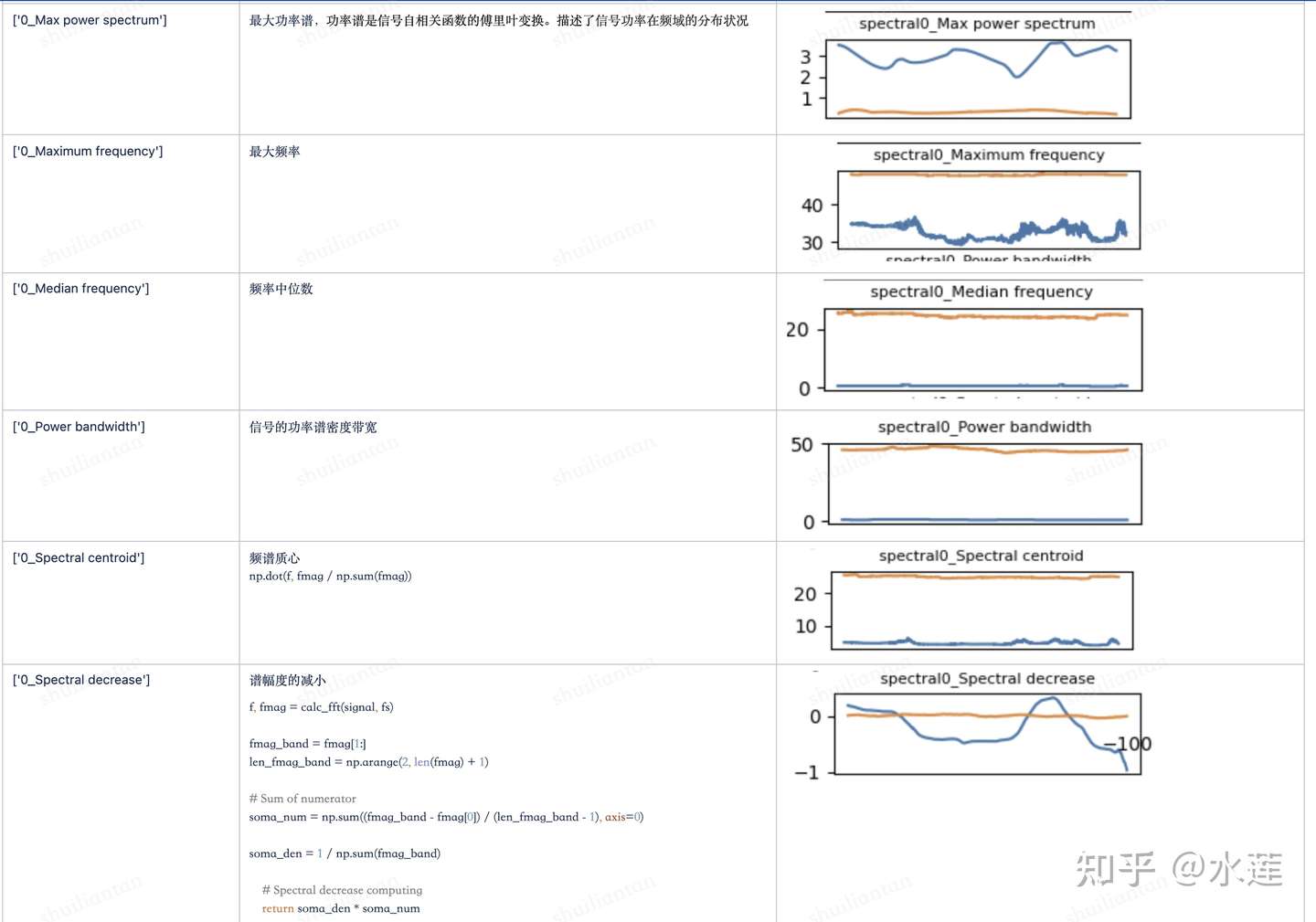

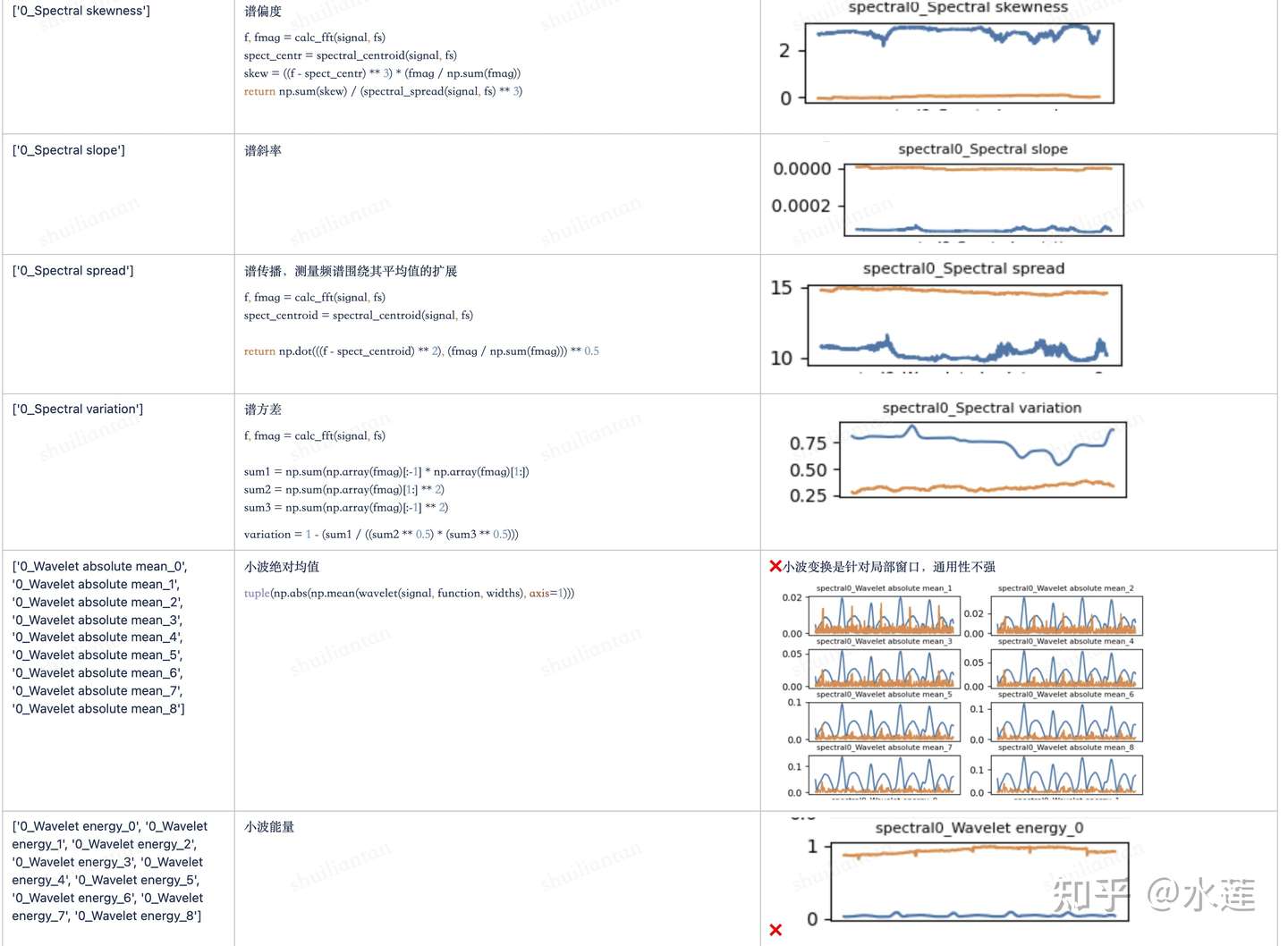

时域类特征
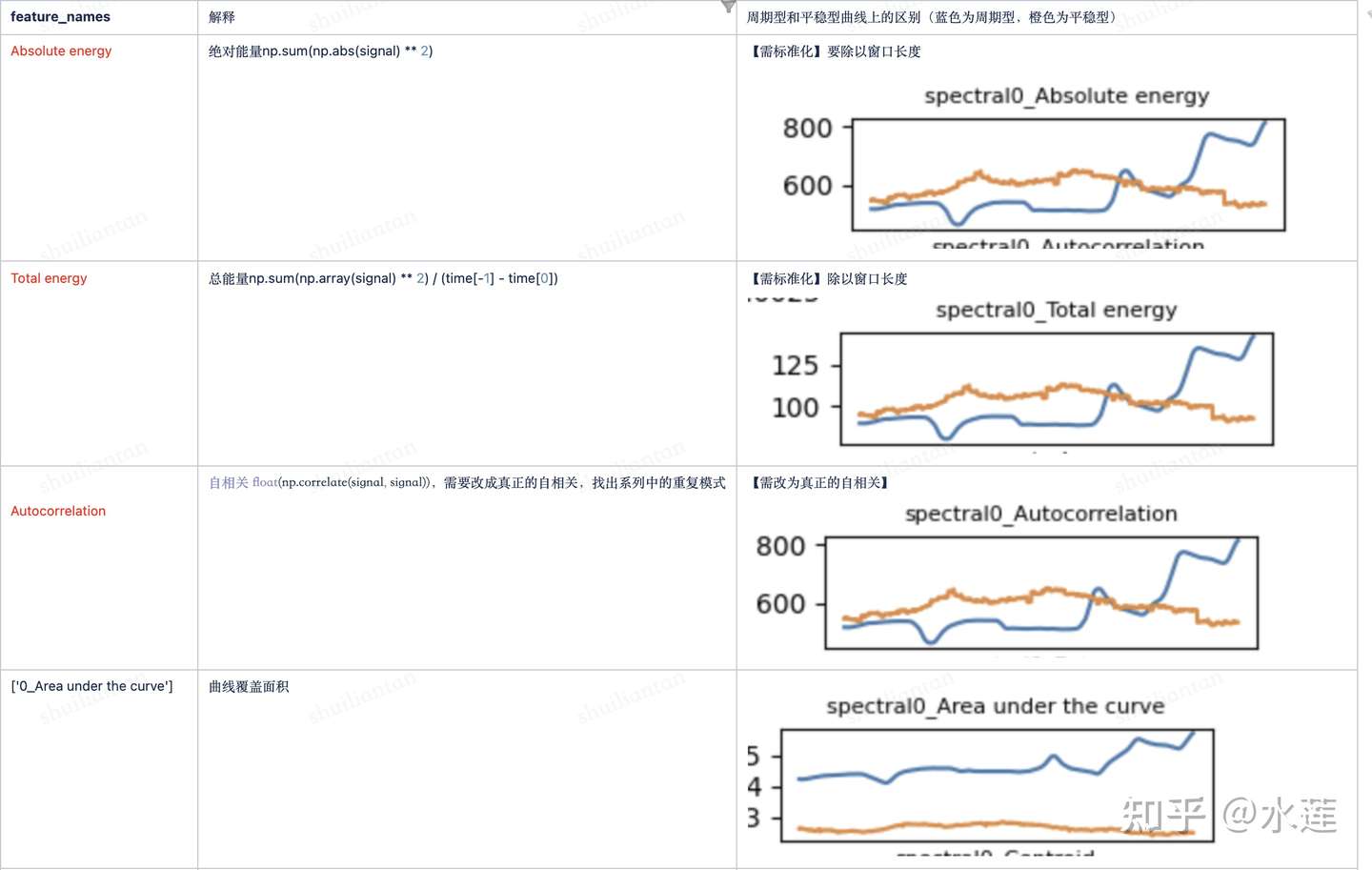
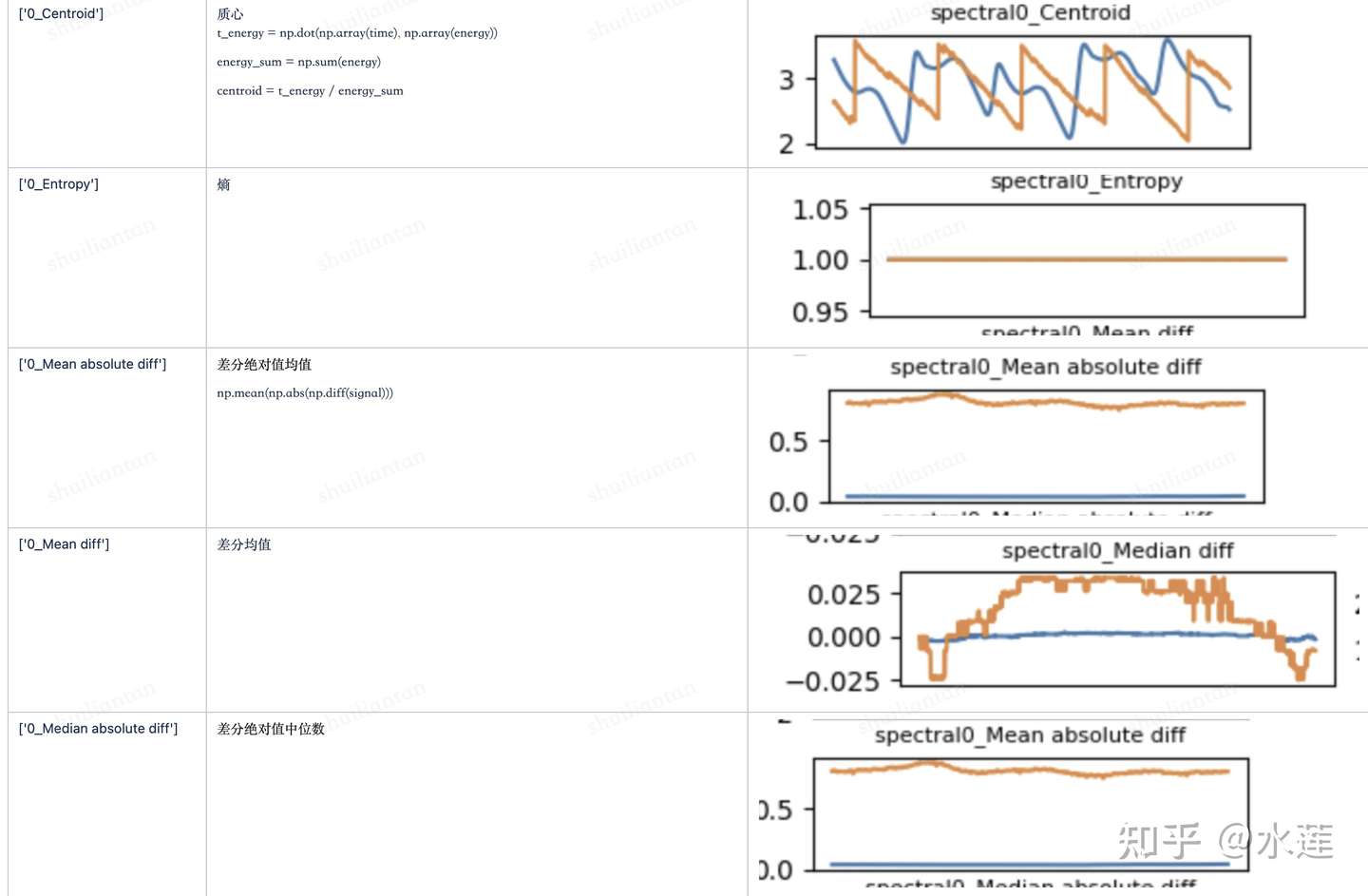
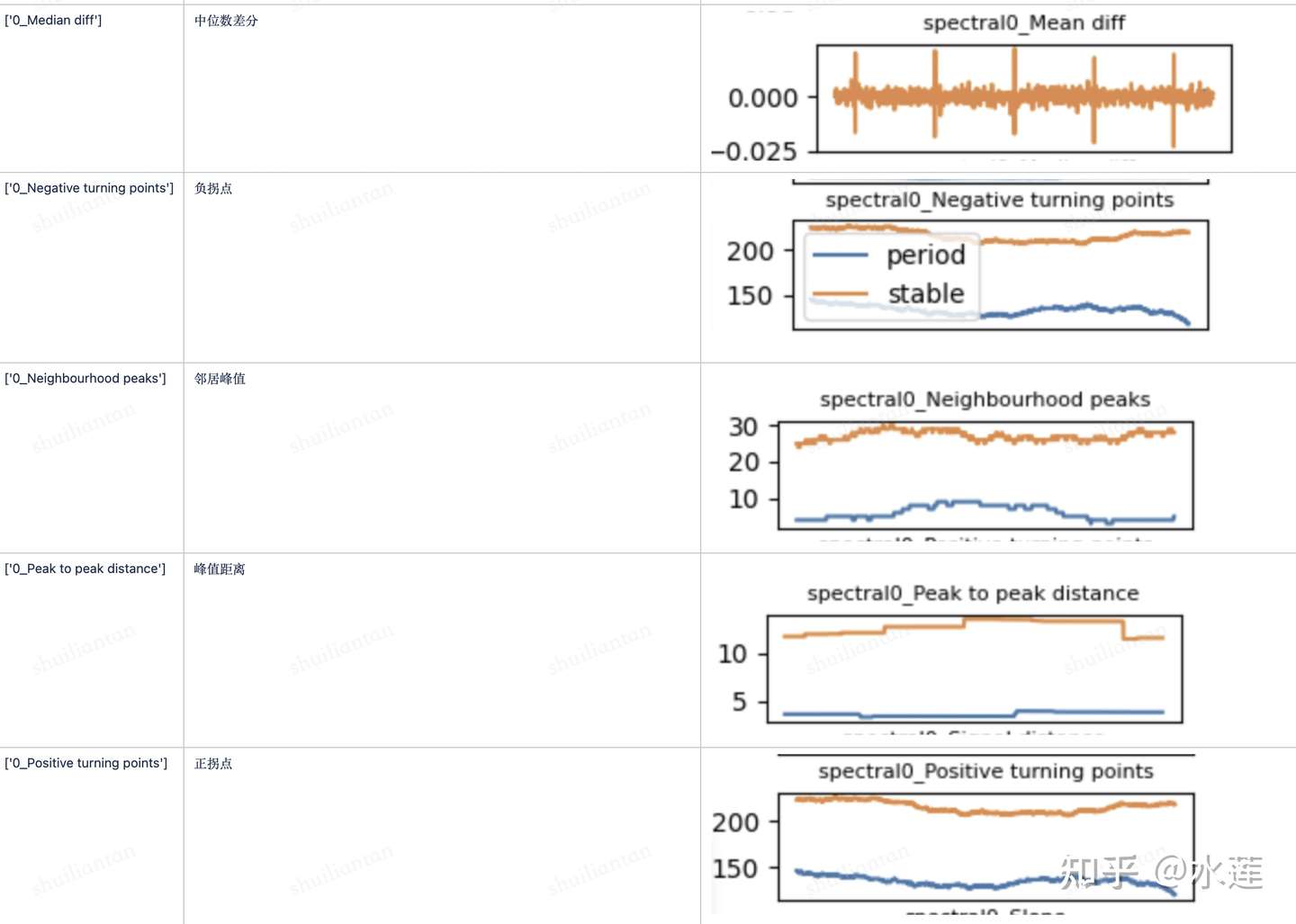
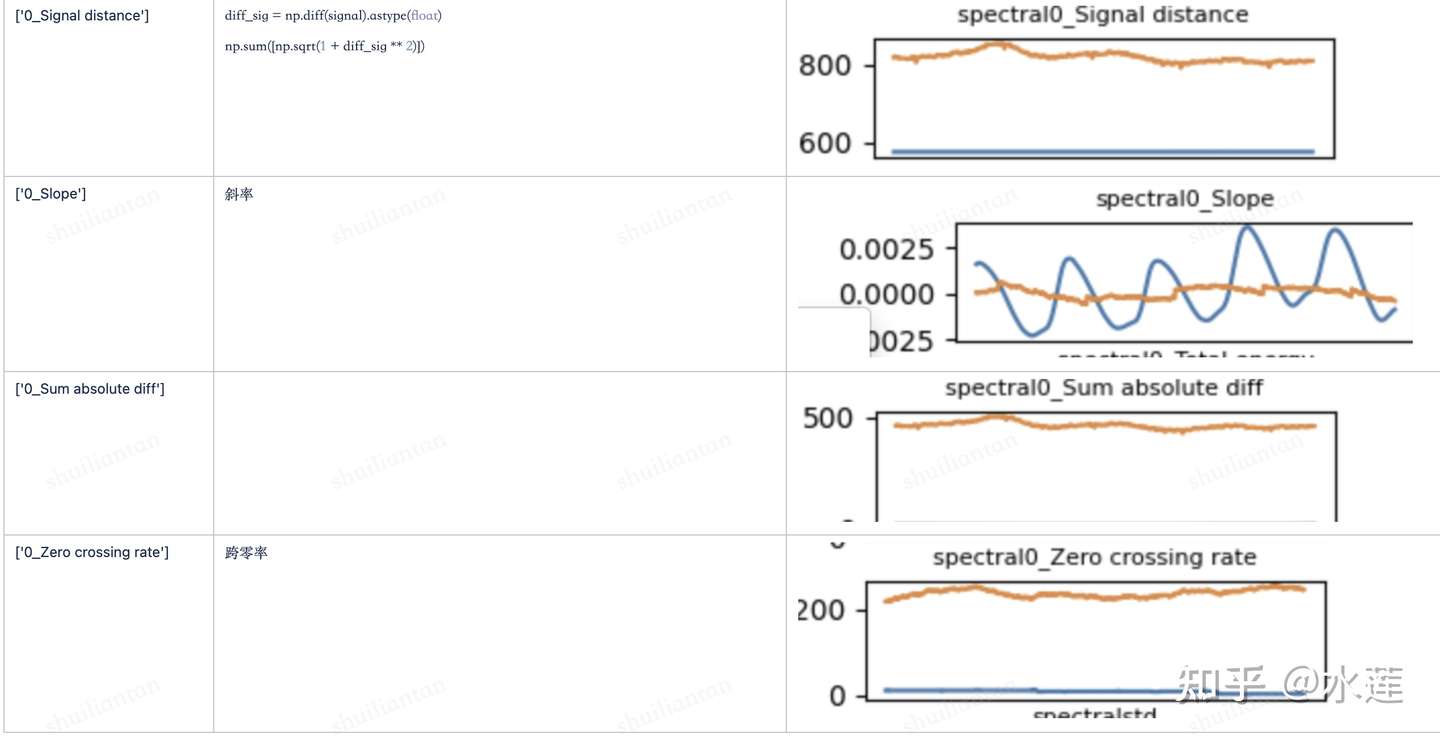
傅立叶原理表明:任何连续测量的时序或信号,都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号,以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。
功率谱的概念是针对功率有限信号的,所表现的是单位频带内信号功率随频率的变化情况。保留了频谱的幅度信息,但是丢掉了相位信息,所以频谱不同的信号其功率谱是可能相同的。
小波变换(wavelet transform,WT)是一种新的变换分析方法,它继承和发展了短时傅立叶变换局部化的思想,同时又克服了窗口大小不随频率变化等缺点,能够提供一个随频率改变的“时间-频率”窗口,是进行信号时频分析和处理的理想工具。
其他时序特征库
FATS [2], CESIUM [3], TSFRESH [4] and HCTSA [5].
