作者：浮生六记
链接：https://www.zhihu.com/question/271654098/answer/2198273249
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

1.定义和几何性质

Jacobian矩阵： :  

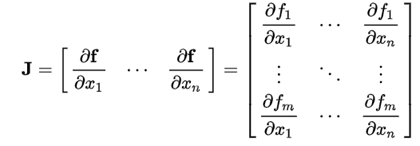
Hessian矩阵：  :  

Jacobian是一阶导数，告诉我们函数如何变化，如果f是标量的话，Jacobian就是一个矢量，指向f增大最快的方向。Jacobian为零的点叫临界点，可能是最大、最小或者鞍点。

f在特定方向e的一阶导数为 

Hessian是二阶导数，相当于曲率，告诉我们函数的凹凸性质，如下图所示：

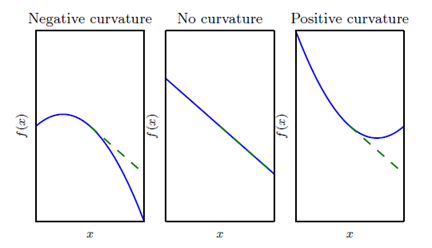
从左到右分别是凹、平、凸，当一个点的Jacobian为0时，可以通过Hessian判断这个点为极大、极小、鞍点。

如果f二阶偏导连续，那么Hessian是对称的，实对称的情况下Hessian可以进行特征值分解，分解为：

 （参见如何理解矩阵特征值？）

f在特定方向e的二阶导数为  。由此我们可以知道在H的特征向量方向的截面的曲率相对应的，就是这个特征向量对应的特征值。如果某个临界点（Jacobian为0的点）处H为正定的话，沿着任何特征值方向这个函数都是凸的，这个点一定是最小值，如果H为负定的话这个局部是凹的这个点一定是最大值，H有为零的特征值或者有正有负的话，无法判断。

2. 利用Jacobian和Hessian进行梯度下降

此时我们考虑 f 是一个值为标量的函数，那么 J 为一个一维向量，H为一个二维矩阵。

最普通版的梯度下降：

加强版：对 f(x) 进行二阶泰勒展开：

使用学习率  ：  ，有：

显然，如果无脑梯度下降，  可能很大，使得这一步更新之后函数反而大了。求一下  这个二次函数的最小值，得到比较合适的更新率：

但是上面还是限制在沿着梯度方向迭代的思路里面，格局小了，Hessian矩阵的条件数（最大本征值和最小本征值的比值的绝对值）很大的时候，沿着不同方向的变化率各向异性很大，梯度的反方向不一一定是长期看来变化最快的方向。

你看，下面这个图里头是沿着梯度方向优化的路线，跌跌撞撞不如直指圆心：

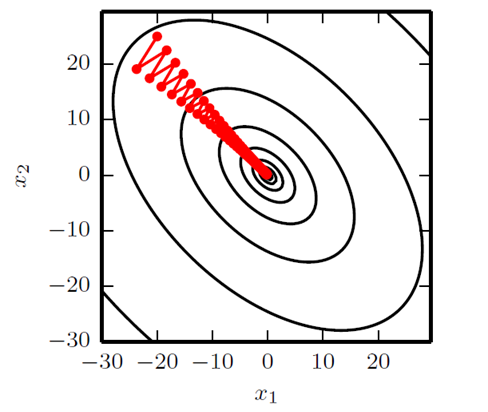
那咋办？我们直接进行一个强制的二阶泰勒级数展开，暴力认为就是一个二阶函数，直接调到二阶函数的极值点去：

极值点为： 

这个就是牛顿法。

（关于梯度下降，我在另一个问题里有一个回答：如何理解随机梯度下降（stochastic gradient descent，SGD）？

关于机器学习和深度学习，我在另一个另一个问题里有一个回答：深度学习与机器学习的关系是什么？）